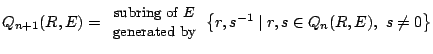 .
.
Then
Javier Sánchez Serdà1
Suppose we have a domain ![]() embedded in a division ring
embedded in a division ring ![]() . We
define inductively:
. We
define inductively:
![]() , and for
, and for ![]()
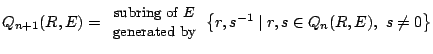 .
.
Then
![]() is
the smallest division ring that contains
is
the smallest division ring that contains ![]() inside
inside ![]() .
We define
.
We define
![]() , the inversion height of
, the inversion height of ![]() inside
inside ![]() as
as ![]() if there is
no
if there is
no
![]() such that
such that ![]() is a division ring.
Otherwise,
is a division ring.
Otherwise,
Let ![]() be a commutative field. Suppose
be a commutative field. Suppose
![]() is a ring
homomorphism which is not onto. Let
is a ring
homomorphism which is not onto. Let
![]() and
and
![]() Consider the skew polynomial ring
Consider the skew polynomial ring ![]() It was proved by Jategaonkar that the
It was proved by Jategaonkar that the ![]() -algebra
generated by
-algebra
generated by ![]() and
and ![]() is a free
is a free ![]() -algebra
-algebra
![]() We call these embeddings
Jategaonkar embeddings.
We call these embeddings
Jategaonkar embeddings.
We prove: