Representations of distributive algebraic lattices by lattices of two-sided ideals
of rings, resp. submodule lattices of modules
Charles University, Prague
We will present some results concerning representations of algebraic lattices in ideal lattices of rings,
resp. submodule lattices of modules. We prove that any algebraic lattice which can be represented
as the lattice of two-sided ideals of some ring can be represented as the submodule lattice of some module as well. Then
we focus on algebraic distributive lattices. An algebraic distributive lattice is determined by the semilattice of its
compact elements and these semilattices correspond to distributive
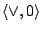 -semilattices.
We present the following results:
-semilattices.
We present the following results:
- Every distributive semilattices which is closed under finite meets is isomorphic to the semilattice of finitely generated
two-sided ideals of some locally matricial algebra.
- Every countable distributive semilattices is isomorphic to the semilattice of finitely generated two-sided ideals
of some locally matricial algebra.
- Every distributive semilattices of size at most
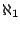 is isomorphic to the semilattice of finitely generated
two-sided ideals of some von Neumann regular ring but there is a distributive semilattices of size
is isomorphic to the semilattice of finitely generated
two-sided ideals of some von Neumann regular ring but there is a distributive semilattices of size 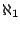 which is not isomorphic to
the semilattice of two-sided ideals of any unit-regular ring, in particular, of any locally matricial algebra.
which is not isomorphic to
the semilattice of two-sided ideals of any unit-regular ring, in particular, of any locally matricial algebra.
- There is a distributive semilattices of size
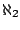 which is not isomorphic to
the semilattice of finitely generated submodules of any module.
which is not isomorphic to
the semilattice of finitely generated submodules of any module.
2005-05-23
![]() -semilattices.
We present the following results:
-semilattices.
We present the following results: