Logaritmic convolution condition for homogeneous Calderón-Zygmund kernel
University of Missouri
Homogeneous Calderón-Zygmund kernel is a convolution
kernel of the type
where 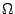 is an integrable function with mean zero on the unit sphere
is an integrable function with mean zero on the unit sphere
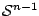 .
It is well known that the
corresponding convolution operator is bounded on
.
It is well known that the
corresponding convolution operator is bounded on 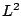 if and only if
the convolution
if and only if
the convolution
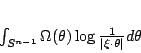 |
(1) |
is essentially bounded. We provide an example that shows that on 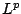 ,
, 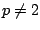 ,
the condition (
,
the condition (![[*]](file:/usr/share/lib/latex2html/icons/crossref.png) ) is no longer sufficient.
) is no longer sufficient.
2005-05-23