A new approach to finite semifields

Simeon Ball

Universitat Politècnica de Catalunya

A finite semifield is a finite set $S$ with two operations, addition and multiplication, such that $(S,+,\circ)$ satisfies all the axioms of a field except (possibly) associativity of multiplication.

A semifield can be used to coordinatise a projective plane of order $\vert S\vert$ and we are interested in finding semifields that produce non-isomorphic projective planes. Two semifields are said to be isotopic if they coordinatise isomorphic planes. There are less than roughly 20 known families of (mutually non-isotopic) semifields. Unless it is immediate that two semifields are not isotopic it is generally difficult to establish whether or not they are. Above all, the goal in this area is to construct many more families of non-isotopic semifields. The first semifields were discovered by Dickson, roughly 100 years ago with more examples given later by Albert (1950's), Knuth (1960's), Cohen and Ganley (1980's) and various families due to Kantor, amongst others, have been constructed in the last twenty years.

If $S$ is finite then it can be shown that $\vert S\vert=q^n$ for some prime power $q$ and that $S$ can viewed as a vector space of rank $n$ over ${\mathbb F}_q$, where multiplication is given by $a_{ijk} \in {\mathbb F}_q$ by the rule

$$e_i \circ e_j = \sum_{k=1}^n a_{ijk} e_k,$$

where $\{ e_1,e_2,\ldots,e_n \}$ is a basis for $S$ over ${\mathbb F}$. Knuth was first to note that any permutation of the subscripts produces another semifield, so there are six semifields associated with any semifield.

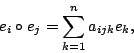
In this talk I shall present a new way to construct finite semifields of order $q^n$ from two subspaces of a vector space of rank $rn$ over ${\mathbb F}_q$, for some $r$. In fact any finite semifield can be constructed in this way for some $r \leq n$, moreover any known semifield of order $q^n$ can be constructed from two subspaces of a vector space of rank $2n$ or rank $3n$ over ${\mathbb F}_q$.

The construction also provides us with a new operation (not one of the six due to Knuth) which produces more semifields in the case when $r=2$.